IN -------[R]------+-----> OUT
|
[C]
|
(GND)
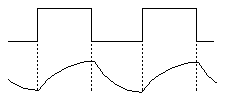
この波形は以下のようになります.

方形波を入れると,積分されたような波形が出てきます. これはどの様な理由によるものでしょうか? 以下のように入力の電圧を V,出力を E とします. またそれぞれの部品のインピーダンスを R, 1/jwC とします.
IN o------[R]------+----------o OUT
A R | 1 A
| [C] --- |
V| | jwC |E
| (GND) |
この回路の伝達関数,つまり出力と入力の関係は以下のような式になります.
V-E E ----- = ------- R (1/jwC) ∴ E 1 --- = --------- V 1 + jwCRここで,jw を S と置き換え,CR を α とします.
E 1 --- = -------- V 1 + Sαここで,ラプラス変換を見ると,この 1/ (1+aS) は一次遅れ要素となります. つまり,このときの周波数特性は下図のような特性となります.
dB
|
|----------+ 1
| \ ------
| \ 1+as
| \
| \
+-------------------------- f
この周波数特性は LPF です.
さて,このどの部分が積分にあたるのでしょうか?
ラプラス変換をみると,積分要素は 1/as となります.
このときの,周波数特性は下図のようになります.
dB
| \ 1
| \ ---
| \ aS
| \
| \
| \
+-------------------------- f
ここで,1/(1+as) の周波数特性を眺めると,ちょうど左斜めの部分が 1/as と同じ感じだということがわかります.
つまり,積分はこの斜めの部分,つまり 1/as にあたる部分になります.
よって,LPF の一部はそのまま積分回路として働くことが理論的にわかると思います.
IN -------[C]------+-----> OUT
|
[R]
|
(GND)
この波形は以下のようになります.
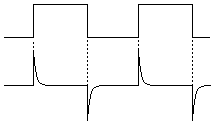
方形波を入れると,微分されたような波形が出てきます. これはどの様な理由によるものでしょうか? 以下のように入力の電圧を V,出力を E とします. またそれぞれの部品のインピーダンスを R, 1/jwC とします.
IN o------[C]------+----------o OUT
A 1 | A
| --- [R] R |
V| jwC | |E
| (GND) |
この回路の伝達関数,つまり出力と入力の関係は以下のような式になります.
V-E E --------- = --- 1/(jwC) R ∴ E jwCR --- = --------- V 1 + jwCRここで,jw を S と置き換え,CR を α とします.
E Sα --- = -------- V 1 + Sαここで,ラプラス変換を見ると,この 1/ (1+aS) は一次遅れ要素となります. また aS は微分要素となります. それぞれの周波数特性は下図のようになります.
dB dB
| | aS /
|----------+ 1 | /
| \ ------ | /
| \ 1+aS | /
| \ | /
| \ |/
+-------------------------- f +---------------- f
この2つの周波数特性を合わせると以下の様になります.
この周波数特性は LPF です.
さて,このどの部分が積分にあたるのでしょうか?
ラプラス変換をみると,積分要素は 1/as となります.
このときの,周波数特性は下図のようになります.
dB | | aS | +--------- ----- | / 1+aS | / |/ +-------------------------- fこの特性は HPF の特性です.